A set of commonly used solutions to the wave equations for laser beam propagation are the Hermite Gaussian functions. This page shows, in quick and dirty fashion, the equations for calculating these functions and some examples of what pure Hermite Gaussian beam profiles (irradiance patterns) look like.

Laser Beam Propagation and the Hermite Gaussian Solutions.

Irradiance profiles of a laser beam on a target can often be expressed as a sum over indices, m and n, associated with the cartesian coordinates on the target surface (x,y).

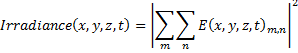
Where we are summing over the electric fields associated with pure Hermite Gaussian modes, each with two indices, m and n.

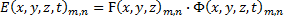
And each field is composed of an amplitude: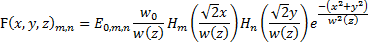 and a phase:.

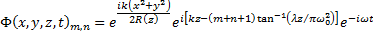In these equations the beam half width as a function of distance from the waist, z, is given by:

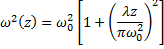
and the radius of curvature is given by:

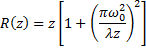
Of course, the one thing left to explain is the Hermite Polynomial, a special function given by the generating function:

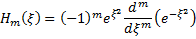
Laser beams are often discussed in terms of the axial modes of the beam, which refer to the wavelengths that can be amplified in the laser cavity, determined by the pumping mechanism, the gain medium and the exact optical length of the cavity. But, the irradiance patterns are determined by the Transverse Modes that are amplified. These transverse modes are what we can represent with the Hermite Gaussian basis set we have developed above.

Following are some images representing some of the pure transverse modes. At the end, I will also show a combination of 2 or 3 transverse modes, which is the more common occurrence in real lasers.

First we will start with the transverse mode that most laser manufacturers (excepting special reasons) strive for, The TEM00 mode.

TEM00

TEM01

TEM10

TEM11

TEM21

TEM12

TEM22

TEM02

TEM20

TEM33

TEM44

TEM55

TEM 11, 11

A combination of Transverse Modes

I think this gives you an idea of the way these pure modes progress and somewhat of an idea about how they can combine as a basis set to form almost any transverse beam profile you can find in a laser beam.