Quadratic Formula

The derivation of the quadratic formula

This is the most popular method for solving quadratic equations since it is easy to remember and applies to many quadratic equations that arise in science, engineering and even finances.

Many science and engineering problems produce quadratic equations that must be solved to obtain the desired answers. Most scientists and engineers immediately use the quadratic formula to quickly solve such equations. Generally they have this formula memorized and write it down without much thought. It is a great tool and can be applied to so many situations that it is worth memorizing.

In this article, we will show how to derive the quadratic equation and then show a couple of examples of how to use it.

A quadratic equation is an equation that can be put in the form:

$$a{x}^2+bx+c=0$$

Where $x$ is the unknown variable and $\mathrm{a,}$ $b$ and $c$ are the known coefficients. It is called “quadratic” because it is a second order polynomial equation in a single variable. In other words, there is an unknown variable of second degree or raised to the power $2$. The word, “quad…” actually refers to squares which have 4 sides, but you “square” the length of one side (meaning raising it to the power 2) to get the area of a square.

Scientists, engineers and a whole bunch of high school students are very familiar with the quick solution to a quadratic equation called the quadratic formula. The formula looks like this:

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

There is a slight catch.... it won't work in the case $a=\mathrm{0,}$ but then you wouldn't have a quadradic equation to start with. So, the caveat is: $a\ne 0.$

This is actually two solutions for $x$ in terms of the known coefficients, which is exactly how many solutions you expect for a quadratic equation.

In this article, we will derive the quadratic formula as a solution to the given equation. Deriving this formula is quite easy, but after learning the formula, most people never again bother to think about where it comes from, they just use it.

Let’s start with $a{x}^2+bx+c=0$  and try to solve for the variable, $x$. Our first step is to get the $x^2$  by itself. To do that, we just divide the equation by the coefficient $a$ to get:

$$x^2+\frac{b}{a}x+\frac{c}{a}=0$$

Then we take the resulting constant term to the other side of the equation by subtracting it from both sides

$$x^2+\frac{b}{a}x+\frac{c}{a}-\frac{c}{a}=-\frac{c}{a} \to x^2+\frac{b}{a}x=-\frac{c}{a}$$

Now that we have this equation,

$$x^2+\frac{b}{a}x=-\frac{c}{a}$$

we are going to try to find a solution by “completing the square”. In this case we will add the same term to both sides of the equation. The term we are adding is one that makes the left hand side (LHS) look like the square of a single term.

$$x^2+\frac{b}{a}x+\frac{b^2}{4a^2}=-\frac{c}{a}+\frac{b^2}{4a^2}$$

The reason we chose $+\frac{b^2}{4a^2}$ is because

$\left(x^2+\frac{b}{a}x+\frac{b^2}{4a^2}\right)=\left(x+\frac{b}{2a}\right)\left(x+\frac{b}{2a}\right)={\left(x+\frac{b}{2a}\right)}^2$

So now we can write:

$${\left(x+\frac{b}{2a}\right)}^2=-\frac{c}{a}+\frac{b^2}{4a^2}$$

which gives us a single squared term on the LHS and only known coefficients on the right hand side (RHS).

A solution is fairly easy to arrive at from here since all we need to do is take the square root of both sides. Of course, when you take the square root you must allow for the fact that the thing that was squared could have been either positive or negative and you would have gotten the same value after squaring. To take that into account, we just realize that there are two possible values on the RHS, a positive one and a negative one.

$$\left(x+\frac{b}{2a}\right)=\pm \sqrt{-\frac{c}{a}+\frac{b^2}{4a^2}}$$

Just to make things a little more aesthetically pleasing, we usually reverse the order of the terms under the radical so that it is written:

$$\left(x+\frac{b}{2a}\right)=\pm \sqrt{\frac{b^2}{4a^2}-\frac{c}{a}}$$

Of course, we really don’t want the solution to $\left(x+\frac{b}{2a}\right)$,   we want the solution to  $x$,   so we need to move the constant term on the LHS to the RHS leaving our variable by itself on the LHS:

$$x+\frac{b}{2a}=\pm \sqrt{\frac{b^2}{4a^2}-\frac{c}{a}}\to x+\frac{b}{2a}-\frac{b}{2a}=-\frac{b}{2a}\pm \sqrt{\frac{b^2}{4a^2}-\frac{c}{a}}$$

Now we have the variable all alone, but we can clean up the RHS a bit.

Which, finally, reduces to:

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

Which is the only part most people bother to recall.

The Quadratic Equation!

As usual, I have presented this all backwards. What have we just derived a solution to? Let's step back just a little. What our quadratic formula gives us is a quick way to get solutions for $x$ in the given quadratic equation: $a{x}^2+bx+c=0$. These solutions are often referred to as the "roots" of the equation. If we were to graph this equation, we would see that the roots are the points where the graph intercepts the $x$ axi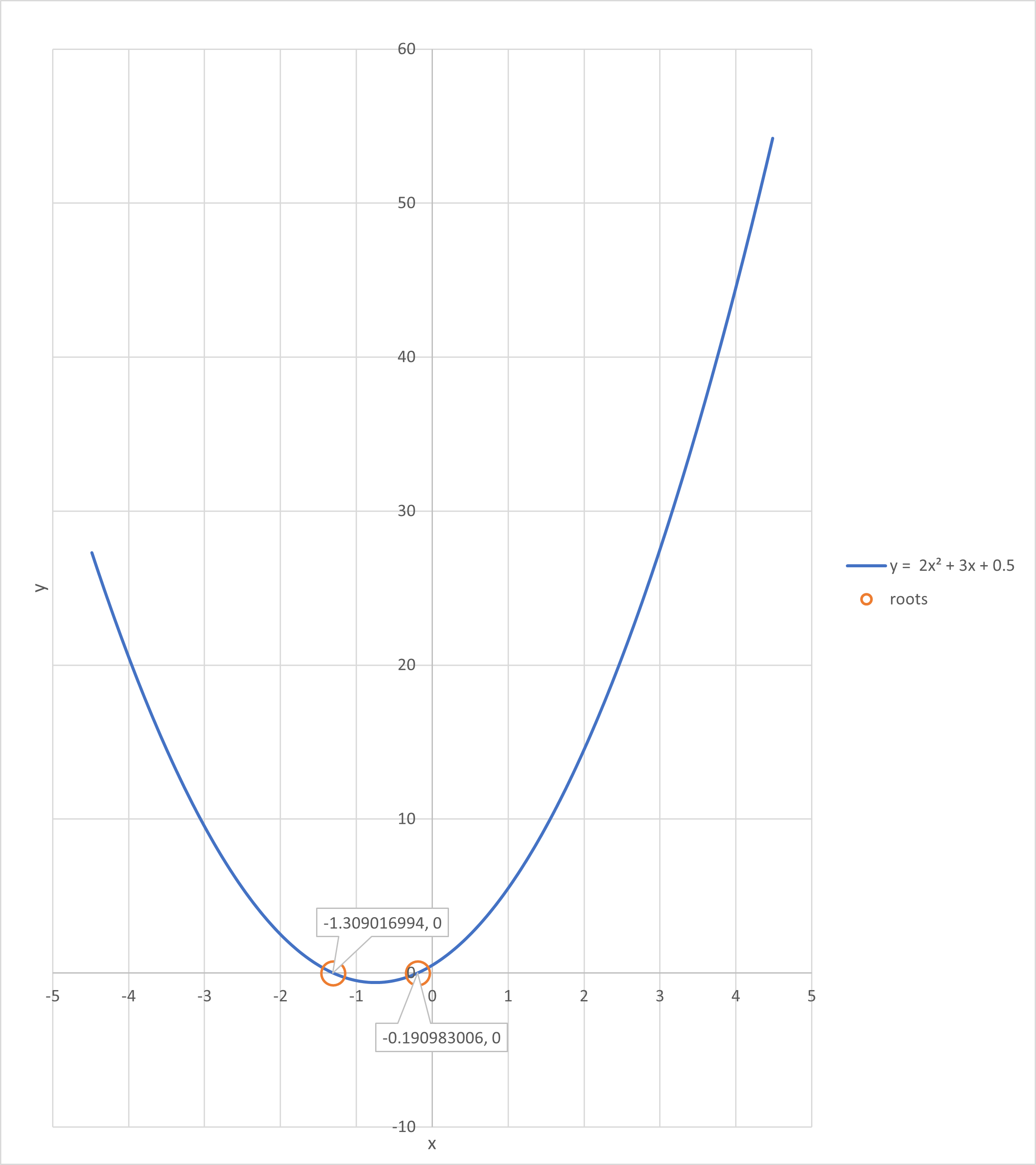s. The graph here is an example, where the equation being graphed is   $y=2x^2+3x+0.5$   so, to find the roots (where   $y=0$ ),   we note that   $a=2$ ,   $b=3$ ,   and   $c=0.5$   and then plug these values into the quadratic formula to get: $$x=\frac{-3\pm \sqrt{3^2-4\times 2\times \mathrm{0.5}}}{2\times 2}$$ Which works out to be   $y=0$   when   $x=\frac{-3-\sqrt{5}}{4}$   or   $x=\frac{-3+\sqrt{5}}{4}$.  

Some Fun with Roots

The Descriminant and the nature of the roots

The value under the radical sign is referred to as the "Descriminant": $D=b^2-4ac$.   The value of this descriminant relative to zero will tell a great deal about the nature of the roots.

• $D>0,$   the roots are real and distinct
• $D=0,$   the roots are real and equal
• $D<0,$   the roots are complex (having imaginary components)

Sum & Product of Roots of the Quadratic Equation

If we give names to the roots of the equation: $$\alpha =\frac{-b+\sqrt{b^2-4ac}}{2a}, \beta =\frac{-b-\sqrt{b^2-4ac}}{2a}$$ Then we have the sum of the roots: $$\alpha +\beta =\frac{-b}{a}$$ and the product of the roots: $$\alpha \times \beta =\frac{c}{a}$$

You can write a quadratic equation given the roots:

If we start with our quadratic equation in this form:   $a{x}^2+bx+c=0$ then divide the whole equation by   $a$   we have it in this form:   $x^2+\frac{b}{a}x+\frac{c}{a}=0$   but we learned from our sum and product of the roots that these new coefficients can be written in terms of the roots themselves:   $$x^2-(\alpha +\beta )x+\alpha \beta =0$$

Applications

An obvious question is "When do such equation come up? Other than math class."