The Sobel Operator used in image processing

The image above is the result of using the edge finding operator on the black and white image below. This happens to be sunset at El Capitan beach which is right on my way home from work every day. Unfortunately, I can't take credit for getting the photo, since I stole it from a web search for sunsets.

Below is the original image in color:

Here is how this edge finding operator works. Essentially, the operator is a discrete differentiation operator which means that if images were completely continuous, as we imagine them to be in nature, you would be finding the edges in an image by taking a derivative in two dimensions, or the gradient as it is called, which gives you the rate of change of intensity in the image and the direction of greatest change. Anywhere that a discontinuity occurred in the image, you would get a large signal in the derivative. Since the images that we normally work with on a computer are stored in discrete pieces called pixels we have to use a discrete form of the derivative.

We begin by looking at our image as a matrix. To simplify things a bit we will assume our image is black and white -or rather, shades of grey- which we can get for any image by averaging the three different values of intensity, each one representing the intensity of a component color, to get a simple two dimensional matrix where each value in the matrix represents the grey-scale intensity for one pixel in the image.

Now, if we take this 2-D matrix where each value in the matrix represents an intensity (usually a number from 0 which is black, to a maximum of 255 which is white) and we display it we get a typical black and white image like:

M =

If we call our matrix M, then each pixel can be indicated by 2 indices representing the number of pixels from the top left corner with the first index representing how many pixels in the vertical direction down from that corner and the second index representing how many pixels to the right from that corner. We will use the indices, j and i with j giving us our vertical index and i giving us our horizontal index. In our case we have the horizontal values, i, running from 1 to 500 with our vertical values running from 1 to 375. So, any intensity value is indicated by the number assigned to a matrix value.

The Sobel operator consists of two more 2-D matrices, each one is only a 3 ˣ 3 matrix:

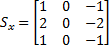  and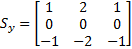  

Finding the gradient in our image can be done for every point in the image as long as it has all eight neighbors. The gradient values form a new matrix which is the convolution of these two 3 ˣ 3 matrices with the image so that the matrix representing the gradient values is given by:

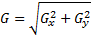  where 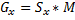    and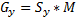  

And the matrix representing the direction of the gradient (Which I don't actually use in this article) is given by:

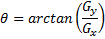
To show you a little more specifically the way I do the convolution and get the gradient values in a form that I can display showing the outlines, I'll write down the same information as above only using the index notation that I normally work with when telling the computer what to do.

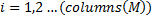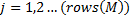
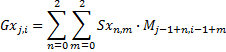  and  

  and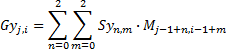  

So that I get the value for each element of my gradient matrix from:

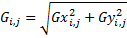
Now I have the magnitude of the gradient corresponding to each point (pixel) in my image. In order to display this set of values, which turns out to dramtically show the outlines of objects in the image, I have to scale this gradient matrix to fit a grey scale image. To do this I just multiply each value by the maximum grey scale (254 is what I usually use) and divide by the maximum value in the gradient matrix. This way, I get a very high value for places in the image where the intensity was changing rapidly as you find at an edge of an object.

This is a fun operator to apply to pictures of your friends. It is almost as much fun as applying fourier optics transforms and filters, which I'll have to show you in another article.