Have you ever wondered just what the probability is of winning the lottery? Actually, they publish the number right on the ticket you buy. But it must be awfully small print because, if you understood that number, you'd certainly nevery waste time or money on a second ticket. On this page we'll show how to calculate that probability and end up with the same number they published. Unfortunately, that number is too small for anyone to really comprehend, since you really don't have any everyday experience to give meaning to such small numbers. Then again, I don't have any experience with the concept of spending $100,000,000 either, but it is fun to think about.

STARKFX.com is usually devoted to science, physics and technology, but something as fun as the math behind finding your chance of winning is just too hard to pass up. So, As a fun study of simple probability (but not psychology) we'll look at the chance of picking a winning lottery ticket in the popular MegaMillions multi state lottery.

Some Basics

Let's start with a few basics before we begin calculating. First, we will only look at winning the jackpot, since that is the only interesting case. Second, you must understand that your chance of winning is not at all influenced by how many players are involved. You are playing against the fates alone and your chances are determined completely by the rules of the game, not by other's participation. Third, we won't judge the moral character of those involved in playing or running this game, after all, it is just a game. However, we may justify the statement that "this game is a tax on those who can't do math", but that would be ignoring some important psychological factors that we just aren't prepared to deal with here.

The Rules

Now the rules: Choose 5 numbers from a pool of 56, then one number from a pool of 46. Note that the order of choosing is irrelevant (that's very important in this case) and that your probability of winning is simply the one (that's how many sets you chose), divided by the total number of possible sets.

So, How Many Possibilities Are There

As you choose your first number you have exactly 56 possible choices. In choosing the second number, you have only 55 possible choices since you already took one out of the pool (you have chosen the first one already so there are only 55 possible choices to take out of the pool now). That means that so far you have:

possible choices.

As you continue to complete your choice of 5 numbers you have:

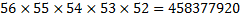
That's four hundred and fifty eight million! That is a lot of possible ways to pick just 5 numbers.

Correction

But we have neglected the fact that the order does not matter, so now we can divide this by the number of ways that this set of choices can be arranged. So, for any particular set of numbers, there were 5 possible choices for the first, 4 possible choices for the second, 3 possible choices for the third, 2 possible choices for the fourth and finally, only 1 choice for the fifth. So the total number of ways to arrange the same set is:

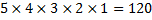
Leaving us with only:

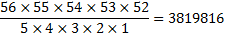
Really, there are only 3.8 million possible choices for our first 5 numbers if we don't care about the order.

Your probability of getting a match for the first 5 numbers is just one out of all of these possibilities:

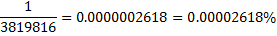
That is twenty six millionths of a percent. -Pretty slim chance!

What we have here is called a combination and can be written as:

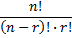
Where n is the number of objects in the pool, and r is the number of objects we can choose without regard to order.
In our case:

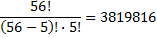
Power Ball

Of course, in the MegaMillions game, we must also choose a power ball, and we have 46 to choose from!

Now our possible choices are:

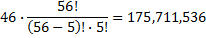
Our chance of winning is one in one hundred and seventy six million!

If you could play this game every second, you could expect to win once in every five and a half years.

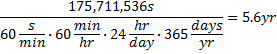
Of course, this would not be a sure thing! Instead, you could buy one hundred seventy five million, seven hundred and eleven thousand, five hundred and thirty six tickets, all with a different number. Yes, this would be a little impractical, and there is always the danger that you may have to share the prize, but you would definitely win. (Be sure the jackpot is at least big enough to pay $176-million in a lump sum payout and I will not take any responsibilty for having given you this idea. This page is for information purposes only and whatever lawyer-type weasel words I need: just imagine them written! -It isn't my fault if you buy 176 million tickets for one drawing and still somehow manage to lose!).

The probability of winning is now one in one hundred seventy five million, seven hundred and eleven thousand, five hundred and thirty six. Well, it isn't quite zero. It is:

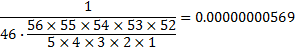
That's 569 billionths of a percent. Next to the 5% success rate of starting your own single proprietorship business, this is certain failure.

But now suppose we buy more than one ticket, say $500 worth.

Now our chances have jumped up to:

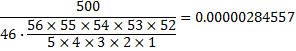
Nearly two hundred and eighty five millionths of a percent! That is: you don't have a chance!

Now suppose we spread our expenditure on this game over many different games. To get at this number, we will calculate our probability of losing on one game with one ticket.

Recall that probability goes from never happens, 0 , to always happens, 1.

Probabilty of losing a game with one ticket:

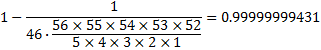
This is just the probability of 1, minus the probability of winning. That is a pretty high percent. But, if I use this to calculate the probability of losing twice in a row we get:

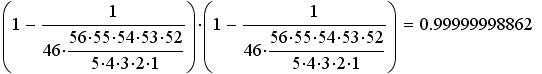
The probability of losing twice in a row is actually smaller. Maybe I could play this game enough times to make the probability of losing, small enough to consider playing. Let's try 50 times in a row.

The probablity of losing 50 times in a row is:

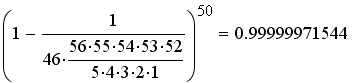
we are making progress.

Let's find out how many times I'd have to play to get even odds, a 50% chance of losing that many times in a row.

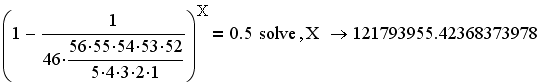
If I play 122 Million games in a row, I have a fifty percent probability of losing, and so a 50% probability of winning. I better get started!