Half way through my undergrad degree in physics, Prof Ostlie looked up from the Quantum Physics course role and, as if noticing my name for the first time, asked, "Mr. Stark, did you know your name was famous in physics? There is an effect with your name on it." I'd never heard of it before and now it was too late to change majors so I thought I'd better find out what it was. This page is a short description of the spectroscopic phenomena observed by Johannes Stark in 1913, the stark effect. Yes, Dr. Stark's work is the only reason this site's name is any good, otherwise I'd have to make my own physics discovery to put my name on.

What is the Stark Effect

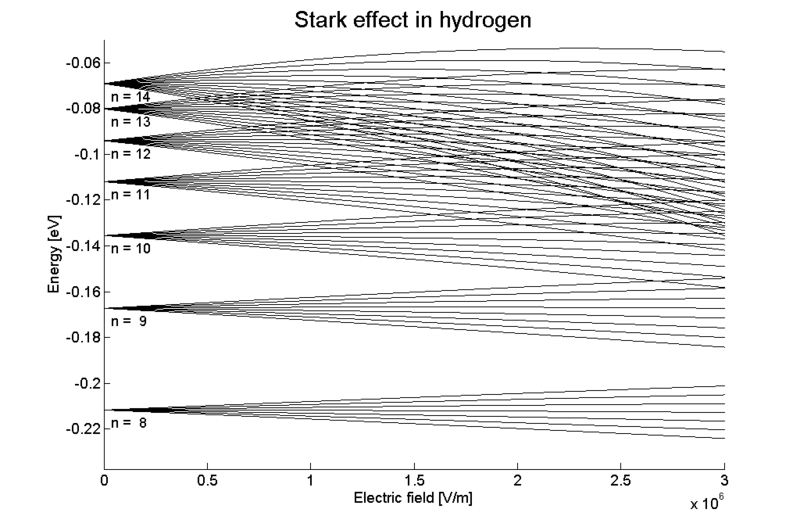The Stark Effect is shown here in the splitting and shifting of spectral lines in hydrogen under the influence of an external electric field.

The stark effect is the shifting and splitting (reduction of degeneracy) of spectral lines in atomic or molecular species under the influence of an externally applied electric field. It is sometimes considered the electric analog to the reduction of degeneracy in atomic and molecular species due to an externally applied magnetic field, the Zeeman effect. I'm not fond of that characterization since the two phenomena are quite different, but it is a reasonable viewpoint.

There are actually two types of stark effect: the linear stark effect and the quadratic version of the stark effect. As expected, the linear stark effect is linearly dependant on the applied electric field while the quadratic stark effect is smaller in the value of splitting and varies as the square of the applied electric field.

---

History of the Stark Effect

When Zeeman discovered the effect of magnetic fields on the wavelengths of emitted spectra from an excited gas, the Zeeman effect, it sparked a search for a similar effect due to electric fields. For fifteen years the search failed to show such an effect and as a matter of fact, Woldemar Voigt of Göttingen (known for the discovery of the Voigt effect) showed on a theoretical basis, with some assumptions, that no such effect should be expected.

Experimental failure to find the effect of electric fields on emitted spectra was actually due to a very simple phenomenon. Excitation of atoms to show spectra was usually performed by passing an electric arc through a gas. The gas would be ionized allowing current to flow via motion of the freed electrons and collisions between electrons and ions or electrons and neutral atoms would excite the ions or atoms and then spectra would be visible as the ions or atoms decayed back down from their excited states. The problem is that applying an external electric field to this highly conductive gas simply rearranges the charges such that the electric field within the gas is neutralized and you have no appreciable fraction of the emitting ions or atoms experiencing any electric field at all. Johannes Stark, in 1913, recognized the importance of lowering the conductivity of the luminous gas in order to maintain a strong electric field within the gas. His method for accomplishing this was to examine the spectra emitted by the luminous canal rays behind a perforated cathode. Goldstein discovered these canal rays were discovered by Goldstein and used by Stark to demonstrate the doppler effect. Stark added a second electrode immediately behind the perforated cathode and applied a strong electric field between this new electrode and that cathode. He found that he could maintain several hundred thousand volts per centimeter between them. He also found that the Hydrogen lines emitted by these canal rays were split into polarized components.

Johannes Stark won the Nobel Prize for his demonstration of the Stark Effect.

When Stark aimed his spectroscope at the region between the electrodes from the side, he found the transverse effect where spectral lines were split into symetrically polarized components on the right and left of the original line. Separation between these components varied linearly with electric field strength, the linear Stark effect. If the field is strong enough, you can also see the quadratic Stark effect in which the separation varies with the square of the applied electric field. With a different arrangement of electrodes, Stark also observed the longitudinal effect parallel to the electric field. Each Balmer line was separated into a number of components. That number increased with the serial number of the line so that the red H line is split into the smallest number (9). Observing perpendicular to the field some of the components seen are polarized parallel to the field while others are polarized perpendicular to the field. Observing in a direction parallel to the electric field, those perpendicularly polarized components appear unpolarized, while the parallel polarized components disappear.

---

Theory of the Stark Effect

The best way to approach the Stark Effect theoretically is by perturbation theory. The idea is that we have the Hamiltonian of the atom or molecule describing the energies and wavefunctions in the absence of an applied electric field and we simply assume that the change in the Hamiltonian, when we apply an external electric field, can be expressed as a smaller "perturbation" on the main Hamiltonian:

Introduction to the Stark Effect

The Stark effect occurs due to the interaction between the electric field and the electric dipole moment of an atom or molecule. When an external electric field is applied, it perturbs the energy levels of the electrons in the atom, leading to shifts and splits in the spectral lines. These changes can be observed using spectroscopy, providing valuable insights into the structure and behavior of atoms and molecules.

Quantum Mechanical Explanation

In quantum mechanics, the Stark effect can be understood using perturbation theory. The Hamiltonian of an atom in the presence of an electric field E is given by:

$$H=H_0+\mathrm{H\text{'}}$$

where $H_0$ is the unperturbed Hamiltonian of the atom, and H' is the perturbation due to the electric field. The perturbation term H' is given by:

H' = -d · E

Here, d is the electric dipole moment operator. For a hydrogen atom, the first-order Stark effect can be calculated by considering the matrix elements of H' between the unperturbed states. The selection rules for electric dipole transitions dictate that only certain transitions are allowed, leading to specific shifts in the energy levels.

Linear and Quadratic Stark Effect

The Stark effect can be classified into two regimes: linear and quadratic. The linear Stark effect occurs when the energy shift is directly proportional to the applied electric field, typically observed in systems with degenerate energy levels, such as the hydrogen atom in its first excited state. The quadratic Stark effect, on the other hand, occurs when the energy shift is proportional to the square of the electric field, commonly seen in non-degenerate systems.

For the hydrogen atom, the linear Stark effect can be observed in the n = 2 state, where the energy levels split into sub-levels due to the electric field. The energy shift ?E for the linear Stark effect is given by:

?E = ± (3/2) e a_0 E

where e is the electron charge, a_0 is the Bohr radius, and E is the electric field strength.

Experimental Observations and Applications

The Stark effect has been extensively studied and observed in various atomic and molecular systems. It has significant applications in fields such as spectroscopy, quantum optics, and laser technology. For instance, the Stark effect is used in Stark spectroscopy to study the electric field distribution in plasmas and to measure the electric dipole moments of molecules.

In modern technology, the Stark effect is utilized in devices like electro-optic modulators, which control the phase and amplitude of light in optical communication systems. Additionally, the Stark effect plays a crucial role in the development of quantum computing and quantum information processing, where precise control of atomic and molecular states is essential.

Conclusion

The Stark effect is a fundamental phenomenon in quantum mechanics that provides deep insights into the interaction between electric fields and atomic or molecular systems. Its theoretical foundation lies in perturbation theory, and it manifests in both linear and quadratic forms, depending on the nature of the system. The Stark effect's applications in spectroscopy, technology, and quantum computing highlight its importance in both fundamental research and practical innovations.

Understanding the Stark effect not only enriches our knowledge of atomic and molecular physics but also paves the way for advancements in various scientific and technological domains.

---

Applications of the Stark Effect

Stark Effect in Quantum Computing

Quantum-Confined Stark Effect (QCSE)

The Quantum-Confined Stark Effect (QCSE) is a specific manifestation of the Stark effect in quantum wells, quantum dots, and other nanostructures. When an external electric field is applied to these structures, it causes a shift in the energy levels of the confined electrons and holes. This shift can be used to control the optical and electronic properties of the quantum dots, which is crucial for quantum computing applications.

Applications in Quantum Computing

Quantum Dot Qubits

Quantum dots can serve as qubits, the fundamental units of quantum information. The QCSE allows precise control over the energy levels of these quantum dots by applying an external electric field. This control is essential for manipulating qubit states and performing quantum gate operations.

Optical Modulation

The QCSE is used in optical modulators, which are devices that control the intensity, phase, or polarization of light. In quantum computing, optical modulators are vital for controlling and routing quantum information carried by photons. The ability to switch optical signals rapidly and efficiently using the QCSE enhances the performance of quantum communication systems.

Quantum Information Processing

The Stark effect enables fine-tuning of the interactions between qubits. By adjusting the electric field, researchers can control the coupling between quantum dots, which is necessary for implementing two-qubit gates and entangling qubits. This precise control is crucial for error correction and reliable quantum computation.

Quantum Sensors

The sensitivity of quantum dots to electric fields makes them excellent candidates for quantum sensors. These sensors can detect minute changes in electric fields, which can be used for high-precision measurements in quantum computing and other applications.

Experimental Techniques

Researchers use various experimental techniques to study and utilize the Stark effect in quantum computing:

• Spectroscopy: By observing the shifts in spectral lines, scientists can measure the effects of electric fields on quantum dots and other nanostructures. This information helps in designing and optimizing quantum devices.
• Electro-Optic Modulation: Devices that exploit the QCSE for modulating light are tested and calibrated to ensure they meet the stringent requirements of quantum computing applications.

Conclusion

The Stark effect, particularly the Quantum-Confined Stark Effect, is a powerful tool in the field of quantum computing. It provides the means to control and manipulate quantum states with high precision, which is essential for the development of quantum computers and related technologies. As research progresses, the applications of the Stark effect in quantum computing are likely to expand, driving further advancements in this cutting-edge field.

---