Welcome to the STARKFX.com Hydrogen Wavefunction Page.!
So, your're sitting around the apartment one day, there is nothin' on the tube, and you start wondering "What are the energy levels of atomic hydrogen? I'd have to know that to figure out the wavelengths of the spectral lines emitted by a hydrogen atom." Then, suddenly, you realize, "Oh my goodness! I'd have to solve the Schrödinger equation and find the the wavefunctions for the hydrogen atom to find out something like that." Then you notice that if you did that you'd also have a way to make some pretty pictures of the wavefunctions and then you could decorate your apartment with something a little classier than that Mandelbrot set on the wall. Well, read on.
If you were just wondering what the energy levels of the hydrogen atom are, and how to find them by solving the Shrödinger equation, you are in luck! On this page, we display the hydrogen atom wavefunctions and energy levels which can be scaled to any hydrogen-like atom (single electron ion).
Hydrogen Atom Wavefunctions
Hydrogen-like atoms, or one-electron ions are the easiest to calculate wavefunctions and energy levels for. (Actually, this is a two body problem which is the only case for which we can find an analytic solution. Any more electrons would just totally mess this up and we'd have to use something awful like perturbation theory). We'll start this calculation by reducing the complexity of our problem from two particles in motion around each other, to just one particle, the electron, in motion about an infinitely massive nucleus (the proton in this case, or the proton with one or two or three neutrons). Just to make things a little more general and to add a lot more excitement, like the possibility of creating photons in the visible, the UV, and even X-ray region of the spectrum, we are going to consider any ionized atom that has just one electron and some number, 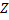 , protons.
, protons.
Writing the Schrödinger Equation of Motion
To accomplish the simplification we mentioned we must use a reduced mass for the electron
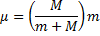 (1) Reduced mass of the electron.
(1) Reduced mass of the electron.
Now we can apply a simple form of the Shrödinger equation which is nothing more than the Hamiltonian for this system of a single particle, the electron, cruising around in a position dependent potential. Of course, we have to know the position dependence of that potential to write the equation and we are in great shape beacause it is just the due to the one over the separation distance squared force between two charged particles.
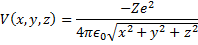 (2) Coulomb potential for our one electron atom.
(2) Coulomb potential for our one electron atom.
Here we have used Cartesian coordinates. 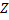 is the atomic number, 1 for hydrogen,
is the atomic number, 1 for hydrogen, 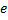 is the magnitude of the charge of either an electron or a proton and epsilon-naught,
is the magnitude of the charge of either an electron or a proton and epsilon-naught, 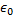 , is the electric permittivity of free space.
, is the electric permittivity of free space.
Next we write the total energy of the system as the kinetic energy plus the potential energy using the momentum squared over twice the mass as the form for writing our kinetic energy.
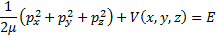 (3) Total system energy.
(3) Total system energy.
OK, we admit that we have totally ignored the gravitational potential between these two particles, and we have assumed other simplifications like no externally applied gravitational field or electric field, but let's just continue on with the assumption that this is all the energy in the system.
Now, we get to apply quantum theory! Dynamical quantities, like total energy and the three cartesian components of momentum will be replaced by their differential operators.
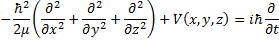 (4) Schrödinger operator equation.
(4) Schrödinger operator equation.
This operator equation must operate on the wavefunction describing the system, 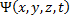 , which is a function of time as well as all three coordinates of space.
, which is a function of time as well as all three coordinates of space.
Making use of the Laplacian Operator, 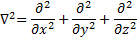 we can write:
we can write:
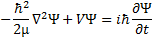 (5) Time dependent Schrödinger equation.
(5) Time dependent Schrödinger equation.
Separation of Variables
Another quick simplification we can make is by use of the fact that, in this formulation, there is no time dependence in the potential energy, it only depends on position. This means that there are solutions to the Schrödinger equation we have written that have the form:
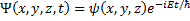 (6) First separation of variables.
(6) First separation of variables.
Now we can write the time independent Schrödinger equation operating on the position dependent (or time independent) eigenfunction which is the solution to the time independent equation.
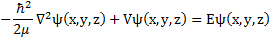 (7) Time independent Schrödinger Equation.
(7) Time independent Schrödinger Equation.
We would like to solve this time independent equation by use of separation of variables but, the potential is a function of all three cartesian coordinates and will not cooperate with our plan. Instead, we need to make a change of coordinates. It just so happens that a nice spherical coordinate system would lend itself perfectly to the potential we are dealing with.
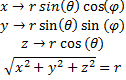 (8) Cartesian to Spherical.
(8) Cartesian to Spherical.
This way our potential energy function can be written:
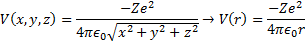 (9) Potential in Spherical Coordinates.
(9) Potential in Spherical Coordinates.
This is a nice simplification, but nothing is ever free! Now we have to write our Laplacian a little different.
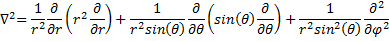 (10) Laplacian in Spherical Coordinates.
(10) Laplacian in Spherical Coordinates.
We still have the same Schrödinger equation, just in a new coordinate system.
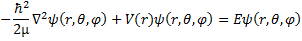 (11) Schrödinger equation in Spherical Coordinates.
(11) Schrödinger equation in Spherical Coordinates.
With our Laplacian written in spherical coordinates, we can now try to find solutions of the equation of a separable form:
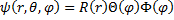 (12) Separable Wavefunction.
(12) Separable Wavefunction.
Let's substitute our separable form of the solution,(12) into the equation, (11) and use the spherical form of the Laplacian, (10) and then we will have to do a little algebra.
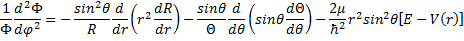 (13) Solve for Phi .
(13) Solve for Phi .
OK, now that we have gone through all that algebra, we have an equation with a function of only azimuthal angle on one side and functions without any dependence on azimuthal angle on the other side. That means that the value that they share must be a constant! Wow, are we lucky that worked. It so happens that we have the guidance of people that have done this before, and so we can learn from their experience and choose carefully a symbol for the shared constant, namely minus m sub l squared
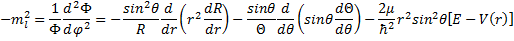 (14) Choose a Constant .
(14) Choose a Constant .
There is a reason we have chosen a negative constant. There is also a reason we have assumed a squared value and assigned the subscript, but all of the reasoning behind these choices will have to wait for a few paragraphs. For now, we will do a little algebra and end up with:
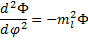 (15).
(15).
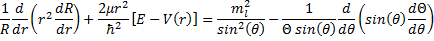 (16).
(16).
Now we have another equation with functions of one variable on one side and functions of a different variable on the other side. So, we can set both sides of this equation to a constant just like we did before. And, just as before, we have the advantage of foresight (since others have done this for us before) and we will choose a particular form for the constant.
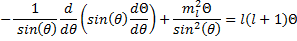 (17).
(17).
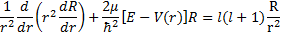 (18).
(18).
This might be a good point to take a look at the coordinate system we are using to find positions in space relative to the postion of the nucleus of our atom.
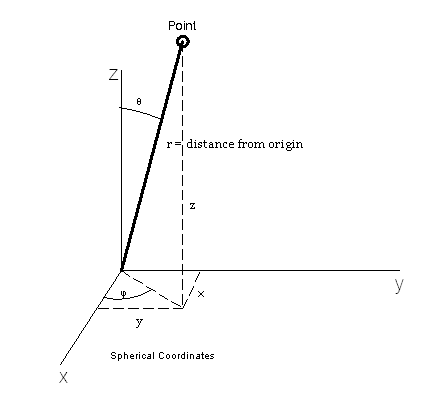
The coordinate triplet 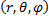 represents the radial distance, zenith and azimuth as shown in the figure. Of course, there is no real way to tell the difference between one direction or another from just the electric field except for the direction of increasing radial distance. But, we need these coordinates for our mathematical description.
represents the radial distance, zenith and azimuth as shown in the figure. Of course, there is no real way to tell the difference between one direction or another from just the electric field except for the direction of increasing radial distance. But, we need these coordinates for our mathematical description.
Azimuth
Let's work on equation (15) first, 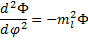 . This is a second order, linear differential equation in the single variable φ with the simple requirement that we get the same value when φ=0 as we do when φ=2π, or in more compact notation:
. This is a second order, linear differential equation in the single variable φ with the simple requirement that we get the same value when φ=0 as we do when φ=2π, or in more compact notation: 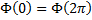 .
.
The common method for solving this equation is to substitute:
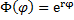
Which leads to the characteristic equation:
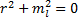
This leads us to the roots:
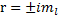
So, we have the solution: 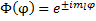
Now we can apply our condition that the value must be consistent between two different representations of the same point and we get:
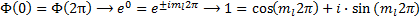
Which is satisfied for 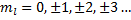 , or, in other words, m sub l is an integer.
, or, in other words, m sub l is an integer.
Zenith
Now, we are left to find solutions to equations (17) and (18) above. We will start with the angular equation for the azimuth dependence, (17), and the first step will be to re-write the equation in terms of an independent variable, z as:
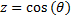
Taking advantage of 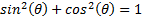 we can see that:
we can see that:
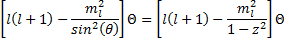
Using 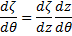 &
& 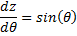 , we can write:
, we can write:
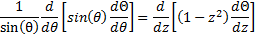
So, we can finally rewrite (17) as:
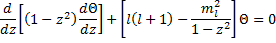
Had you been paying attention in your differential equations class, you would immediately recognize this as a form of the Legendre Equation:
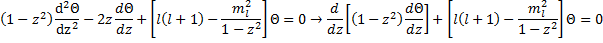
the canonical solutions to which are the Associated Legendre Functions where the indices 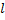 and
and 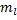 are the degree and order respectively of these functions.
are the degree and order respectively of these functions.
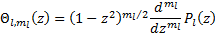 (19).
(19).
Where 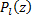 are the Legendre Polynomials.
are the Legendre Polynomials.
Recall that the Legendre polynomials begin with 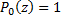 and
and 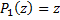 and then use the recursion relation:
and then use the recursion relation:
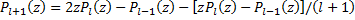
then, we just do algebra until we turn blue --I mean until we get to the degree that we want. These polynomials start to look very dull and, while your eyes are glazing over, you'll notice that they do alternate between even and odd powers of the variable. Now, if we pay a little more attention to equation (19) we see that since the highest power of any Legendre polynomial is the degree so that the order must be less than or equal to the degree 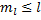 or else our derivatives will drive our function to zero.
or else our derivatives will drive our function to zero.
We want to quickly take a look at another formula for the Legendre Polynomials, namely Rodrigues' formula, since it is useful in clearing up a little ambiguity.
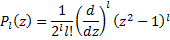 Rodrigues' formula.
Rodrigues' formula.
Notice that equation (19) might suggest to you that 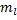 cannot be negative, since you probably aren't used to taking negative order derivatives. But, if we use Rodrigues' formula, then our derivatives are not of negative order unless
cannot be negative, since you probably aren't used to taking negative order derivatives. But, if we use Rodrigues' formula, then our derivatives are not of negative order unless 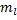 is larger than
is larger than 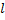 . So, we can now put a boundary on the order of the function:
. So, we can now put a boundary on the order of the function: 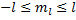 . Then, using Liebnitz's differentiation formula:
. Then, using Liebnitz's differentiation formula:
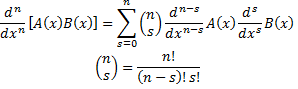 Liebnitz's differentiation formula.
Liebnitz's differentiation formula.
we can show that: 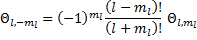
For just a moment, we need to step back and look at the differential equation that must be solved by the Legendre polynomials themselves:
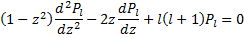
Assuming a series solution to the polynomial: 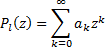
We insert this series solution into the differential equation that it must solve and then combine like terms and we get:
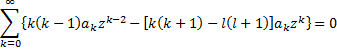
Writing out a few terms and then rewriting to show a common power of z, we get:
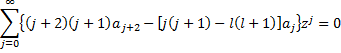
For the equality to hold, the coefficient of each power of z must vanish, which gives us the recursion relation:
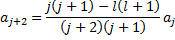 Recursion Relation
Recursion Relation
We get two independent series, one with the odd powers and one with the even powers, all because the recursion relation involves coefficients with indices differing by 2. Each series starts with an arbitrary coefficient, the one with index 0 and the one with index 1 while all other coefficients are determined by the recursion relations for the respective series. Either series gives us a polynomial that goes to infinity as z approaches plus or minus 1, which is a very unacceptable situation for a real physical description. To avoid this situation, we can set one of the arbitrary coefficients to zero, thus eliminating one whole series while we force the other series to remain finite by requiring that 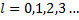 be an integer. To get the complete set of polynomials, we alternately set the first coefficient of the even series to zero and the the first coefficient of the odd series to zero while keeping the requirement that
be an integer. To get the complete set of polynomials, we alternately set the first coefficient of the even series to zero and the the first coefficient of the odd series to zero while keeping the requirement that 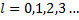 be an integer which terminates either series at the
be an integer which terminates either series at the 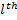 term. For our pursposes we will choose the arbitrary coefficient in each case, so that the powers of z are multiplied by simple integers, which means our functions are not normalized.
term. For our pursposes we will choose the arbitrary coefficient in each case, so that the powers of z are multiplied by simple integers, which means our functions are not normalized.
A set of solutions has emerged from this exercise:
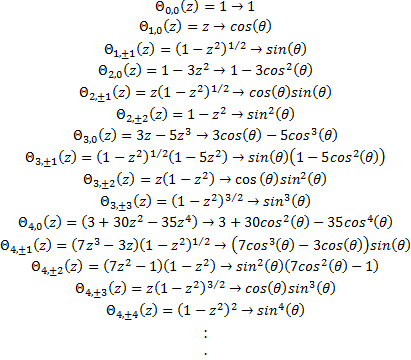
Radial
Finally we need to solve for 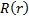 . The differential equation we are looking for a solution for is (18) and if we fill in for the potential given in (9), we have:
. The differential equation we are looking for a solution for is (18) and if we fill in for the potential given in (9), we have:
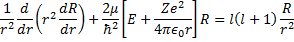
If we multiply through some of the terms, and then make the following substitutions we can simplify this equation a bit.
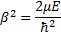 and
and 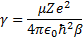 and
and 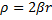
Gives us:
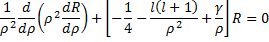
We cannot immediately jump to a series solution for this equation because we get a recursion relation with too many (more than two) of the constants in the series. Instead, we will first look at the case when 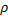 is very large. In that case, the second and third terms in the brackets go to zero leaving us with:
is very large. In that case, the second and third terms in the brackets go to zero leaving us with:
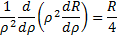
We can quickly see that 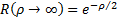 is a solution to this equation that remains finite at large values of the radius, so we need to start looking for solutions that include this insight:
is a solution to this equation that remains finite at large values of the radius, so we need to start looking for solutions that include this insight:
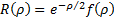
so, substitution of this form into our equation gives us an equation for 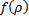 .
.
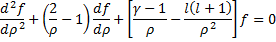
Now we can assume a power series solution for this function:
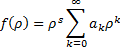 with
with 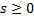 &
& 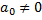
Substitution into the differential equation yields:
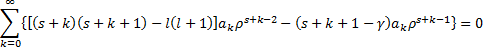
With this little result, we are ready to do a whole bunch of algebra. We will start by pulling out the k=0 term.
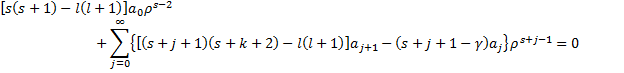
This equation suggests two separate conditions in order for the equality to hold. The first is that the coefficient in the first term is zero, while the second is expressed as recurrence relation for the coefficients in the series.
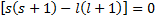 indicial equation.
indicial equation.
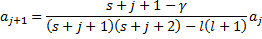 recursion relation.
recursion relation.
The indicial equation is a quadratic equation with two roots. 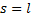 and
and 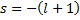 . But, since we know that s must be positive for us to get a finite value at
. But, since we know that s must be positive for us to get a finite value at 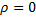 we can accept only the first root.
we can accept only the first root.
So, since we know that 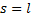 , we can fill in this result in the recursion relation to get:
, we can fill in this result in the recursion relation to get:
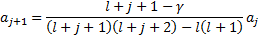
Notice that as 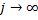 , then
, then 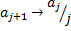 . This is easily recognized by anyone that ever studied calculus as the same ratio of coefficients seen in the Taylor Series expansion of the exponential function,
. This is easily recognized by anyone that ever studied calculus as the same ratio of coefficients seen in the Taylor Series expansion of the exponential function, 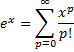 . So,
. So, 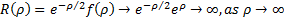 . Here is where we play a wonderful little trick. We simply assert that an infinite result is not physically possible, so our series expansion,
. Here is where we play a wonderful little trick. We simply assert that an infinite result is not physically possible, so our series expansion, 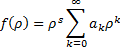 , must terminate rather than be infinite. It just so happens that it will terminate if we demand that
, must terminate rather than be infinite. It just so happens that it will terminate if we demand that 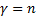 , where
, where 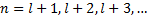 and with
and with 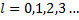 . Doing this causes the series to terminate at the
. Doing this causes the series to terminate at the 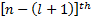 term. So now we can show that
term. So now we can show that 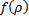 is a polynomial of order
is a polynomial of order 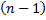 .
.
We have already determined that 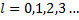 must be an integer to keep our function of the zenith angle finite, and now we have a requirement that n is an integer which actually constrains the possible values of l,
must be an integer to keep our function of the zenith angle finite, and now we have a requirement that n is an integer which actually constrains the possible values of l, 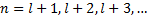 . This leads to the one electron atom energy quantization equation:
. This leads to the one electron atom energy quantization equation:
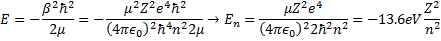
Here is a graph showing the Coulomb potential as a function of radial distance between the nucleus and the electron, and the first eight quantized energy levels. Note that the levels get closer and closer together as they approach zero.
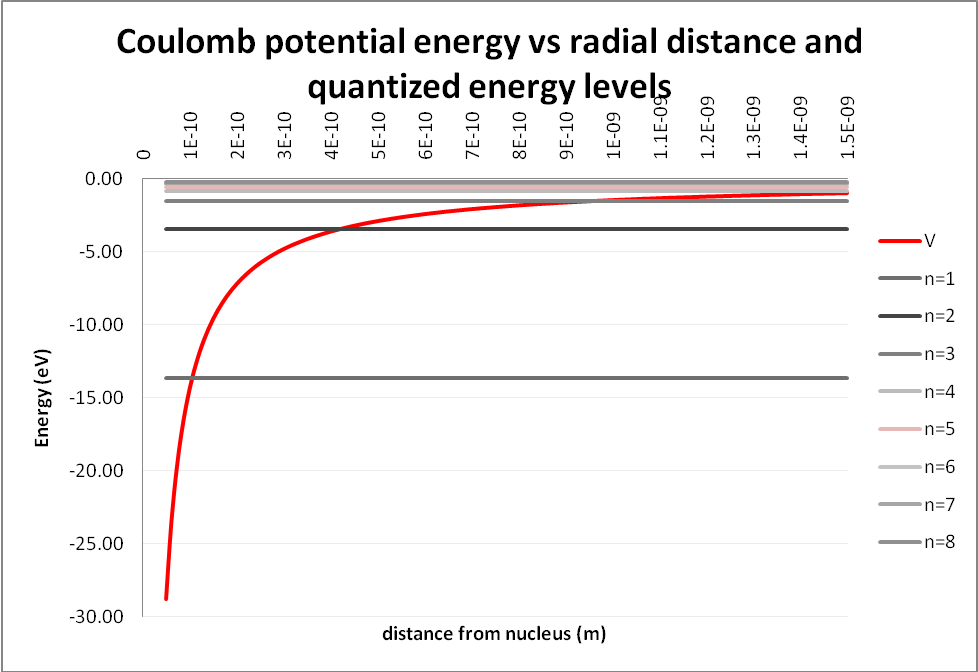
It is convenient to show the higher energy levels on a new chart.
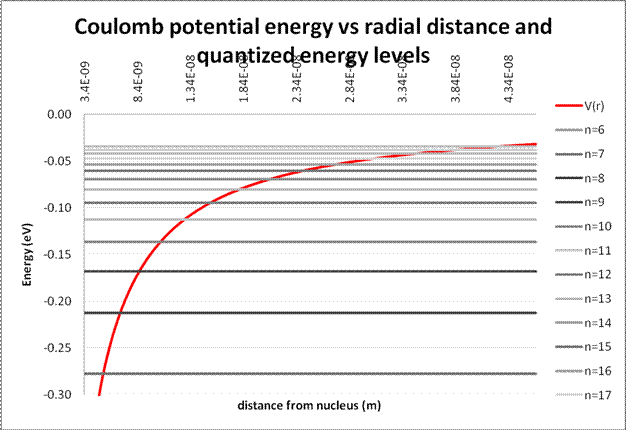
With the information we have now, we can calculate some interesting things:
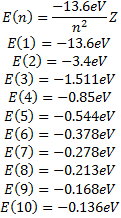

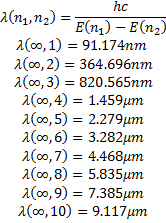
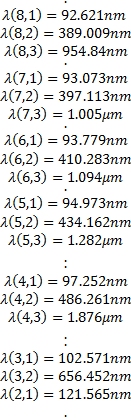
The functions we have found for the radial dependence, also depend on the specific solution we are using for the zenith angle dependence so our radial functions can be written as:
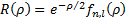
with
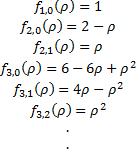
Where, again, the arbitrary constant has been adjusted to get the simplest looking formula. These polynomials are closely related to the associated Laguerre polynomials
Putting together the Eigenfunctions
When we put all of our functions together we have a nice set of eigenfunctions representing the wavefunctions of the single electron atom -in our case, the hydrogen atom but it could be any atom ionized to the point of having only one electron.
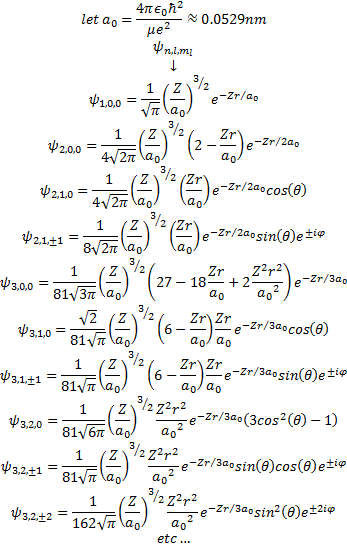
References
- Robert Eisberg and Robert Resnick, Quantum Physics (John Wiley and Sons Inc. 1985).
- George Arfken, Mathematical Methods for Physicists (Academic Press Inc. 1985).
- Erwin Kreyszig, Advanced Engineering Mathematics (John Wiley and Sons Inc. 1993).
You will notice that almost every step on this page has been lifted directly from Quantum Physics, and my only explanation is that this is still my favorite text on the topic. Sadly, I must say, even though I live in Santa Barbara, I've never met Robert Eisberg. I guess I'll have to work on my social skills.
Quick Science & Math References
- Our Solar System.
- Earth Facts.
- The Metric System.
- Trigonometric Identities.
- Vector & Tensor Identities.
- Explicit Forms of Vector Operators
- Light & Electromagnetic Spectrum.
- Common Laser Wavelengths.
- Human Physiology Facts.
- Human History Timeline
- Geologic Timeline
- Cambrian Explosion
- Life on Earth Timeline
- ASCII Codes and HTML Display Codes
- Thousands of HTML Symbol Codes
- HTML Symbol Codes for Greek Letters
- The Best Way to put Equations on your Web Page
Physics Basics Series
- Basics of Classical Mechanics.
- Basics of Quantum Mechanics.
- Basics of Electrodynamics.
- Basics of Optics.
- Basics of Mathematical Tools for Physics.
- Basics of Plasma Physics.
- Basics of Solid State Physics.
Math Basics Series
- Numbers
- Arithmetic
- Algebra
- Geometry
- Analysis
Technology Basics Series
- Basics of Remote Sensing.
- Basics of Digital Signal Processing.
- Critical Electronic Circuits
- Infrared Imaging Basics
Knowledge Branches
- Information Theory
- How Reading Works in the Brain
- Psychology of Learning
- Logic
WORK IN PROGRESS
- What is the Stark Effect?
- The Chemistry of Love &/or Addiction
- Critical Thinking: How to question what you see, read or hear.
- Aristotle's Prior Analytics - the birth of Logic.
- Optical Solutions, lenses that solve problems
- Fractals
- PTC - Photon Transfer Curve or Mean Variance Analysis
- 3-D Noise
- Laser Primer
- Rail Guns
- Special Relativity
- Radar Technology
- Acousto-optic Cells
- Harmonic Generation for Laser Frequency Doubling (SHG) and Tripling -using non-linear crystals.
- Measurement: Accuracy & Precision.
- Things you should know about computer modeling of physical phenomena!
- Giant Magneto-resistance
- Peltier Cooling
- Pyro-Electric Detectors
- Piezo-Electric Crystals
- Laser Speckle
- FFT and DFT the fast fourier transform and the discrete fourier transform
- Fabry Perot Etalon
- The Hydrogen Atom.
- PCA (Principal Component Analysis)
- Energy per mass in fuels such as Hydrogen, Gasoline, Kerosene, HMX etc...
- Nobel prize winning work on the CCD
- How does a CCD work and what are the normal characteristics of a CCD
- Nobel Prize Winning work on Giant Magneto-resistance
- FROG -frequency resolved optical gating
- Optical Wavefront Sensing
- THz imaging and time-domain spectroscopy
- Camera Calibration
- Laser Designators
- Resampling
