A Derviation of the Taylor Series Expansion

An often-used polynomial expansion is the Taylor series. Approximating the value of a complicated function is a very useful technique. The Taylor series expansion serves as a workhorse in many computer programs to approximate functions that would otherwise be very difficult to program. In other words, the programmers (or their technical advisors) did their algebra first, before writing the program in order to make the program run faster or maybe even make it possible.

A Look at How This Expansion is Derived

Series expansions are an excellent way to quickly represent a complicated function as a simple power series. One reason for doing this is to allow a quick, approximate evaluation of the function at given points or to allow a computer algorithm to approximate a function with more speed than it could attain if it were to actually evaluate the function during a process. With that introduction, let’s look at how we derive a Taylor series expansion for a given function.

Suppose you have a function, 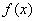, defined for a range of 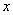values. We would like an approximation for quickly evaluating 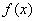, that looks like a simple polynomial with increasing powers of .

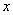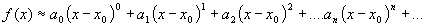
As you can see, the expression would be easy to evaluate, since you only need to get the value 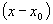one time and if you know the coefficients in front of each power of this term you have it made. Of course, there is the little complication that this series expansion goes on forever, but that is taken care of in many cases by each successive term becoming smaller and smaller so that you have a very good approximation of the value of 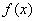after just a few terms. It helps if 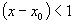so that each successive power is smaller and smaller. Note however, that even if this is the case, the nature of 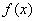still determines if you will “converge” to a good approximation after a few terms of the polynomial.

Let’s proceed anyway and derive a general solution that we can use in the many cases of functions that will produce a polynomial that converges quickly to a good approximation of the function. We start by evaluating our function at 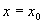which gives us:

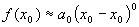
This is the only term left in our series expansion since 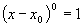for all 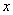including 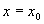while all of the other terms go to 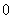for 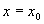. So we have:

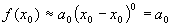
Now we have the first coefficient in our series expansion. It is the value of our function at a point that we know the value.

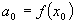
Now we need a way to get the next coefficient and it needs to be a way that eliminates all of the later coefficients in a similar manner to the way we just did for the first one (the zero order coefficient). It just so happens that taking the first derivative of our equation does exactly what we need:

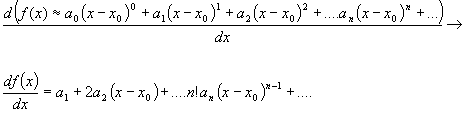
If we evaluate this function at 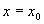we quickly get:

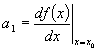
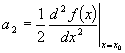
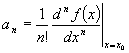
Which allows us to write:

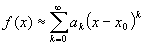
where each coefficient is a derivative another derivative of our function evaluated at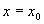

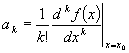
That is the Taylor series expansion of 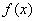with respect to 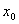for a function of one variable. This series expansion may or may not converge depending on the function but at least now you have an expansion to work with and determine if it will provide the approximation you desire.

By using partial derivatives you can employ the same methods as above to find the Taylor series expansion for a function of several variables. For example, here is the result you will get for a function of three variables, :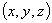

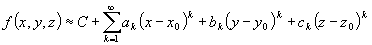
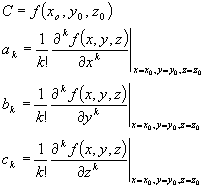
Of course, you are not limited to three variables, you can have as many as you please. The same restrictions apply to your convergence however, and now you must have convergence with respect to all of the variables in order to have a “good” approximation for your function.