Math is infiltrating popular culture. You can't keep up on the latest popular fiction or even Hollywood movies now without being exposed to words from mathematical literature. Well, if you have been reading an otherwise fun book and, suddenly, you came across a reference to the golden ratio, or Φ, perhaps you would like to know a little about what it is. A fascinating number, Φ, derived originally from geometrical considerations, is now the subject of active mathematical research. This page describes just the basics.

This number shows up in nature everywhere. It also shows up in the most interesting human endeavors including aesthetics and now, popular film and fiction.

Φ, (Phi, usually pronounced “fee”). This is a fascinating number. Φ is an irrational number, simply meaning that it can’t be written as whole number or as a fraction using whole numbers. There are other interesting irrationals such as π, but I find Φ to be the most fascinating.

Let’s look first at a geometrical description of Φ. The rectangle below is known as the “most beautiful” rectangle. Divide the width by the height and you get the Golden ratio or Φ.

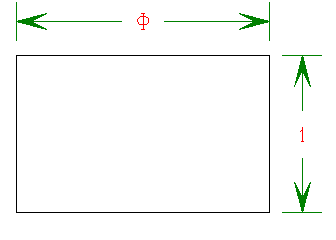  The Most Beautiful Rectangle.

Of course, this is only interesting for the following reason: if you cut off the largest square the rectangle that is left over has the same ratio of lengths.

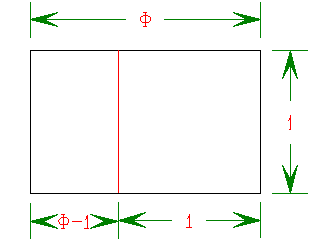
Where .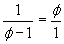
We could solve this and get: 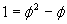or .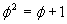
This is an interesting situation. If you solve this, using the quadratic formula, you get:

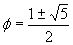
Of course, the situation we have above forces us to accept the + sign in this equation and we get

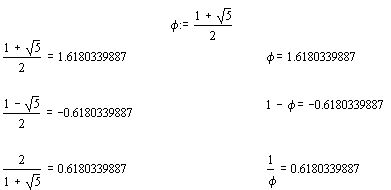
where the decimal representation goes on forever without ever repeating.

While these are rather fascinating to think about, there is an even more interesting way to write this golden ratio. Take the first equation we have above defining the golden ratio 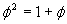and we can take the square root, accepting only the positive root: 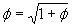but we can substitute for 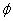on the right hand side to get: 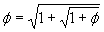but we can substitute for 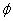on the right hand side to get: 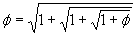and so on forever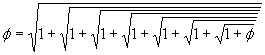

Or, we could have taken 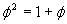and divided by 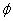to get: 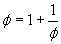and if we iterate substitution the same way as before:
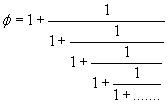
So we found the only irrational number I know of that can be written with nothing but 1’s. Here is what we get if keep the golden ratio on the right hand side:

but if we truncate somewhere along the way, we wont quite reach, but we get closer and closer with each iteration:

Below, I show how I go about constructing a golden rectangle beginning with a 1 ×1 square:

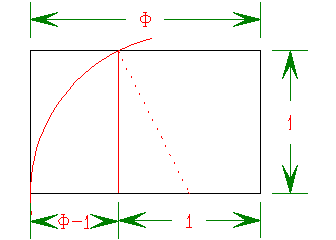
What can you tell about the triangle that is created by drawing my first line from the center of one side of the square to one corner of the square?

Goldene Schnitt

The first appearance of the "Golden Ratio" in any known literature occurs in Euclid's writing circa 300BCE:

"A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lessser."

However, the first recorded use of the term "Golden Ratio" or rather "Goldene Schnitt" is the in the work of Martin Ohm (brother of Georg Simon Ohm, of electrical resistance fame) in his second edition of the book Die Reine Elementar Mathematik (The Pure Elementary Mathmatics) in 1835.

It is probably due to the fascinating properties of the ratio that so many authors have attributed discovery of these properties to cultures from the ancient Egyptians builiding the pyramids to the Babylonians circa 3000 BCE (both of whom definitely did have many important geometrical theories figured out) to Pythagoras himself in ~500 BCE. But the reality is, the first writings showing the properties of this ratio are due to Euclid.