Fibonacci Numbers

Have you heard of Fibonacci numbers before? I know I was well past High School when I first learned of them. That should not have been, but we won’t get into a discussion of what we’re missing in public schools in this little article. Another thing we won’t discuss is the application of Fibonacci numbers to trading in the market. Apparently, that has become a big topic lately. No doubt it does have application to the complex human behavior in the stock market, but I’m not going to attempt to explain that.

History

Leonardo Fibonacci introduced the Fibonacci series in about 1200, in Italy. Leonardo of Pisa, as he is known now, grew up all over the Mediterranean. He was sent as a youngster to learn calculation from an Arab master. Leonardo actually introduced the Hindu-Arab numerals, and the methods of calculating that we are all familiar with now, to the rest of Europe. His books taught business calculation which made them more popular than the more esoteric works read by European intellectuals.

In one of his books, Liber abaci, Leonardo introduced a problem demonstrating the Fibonocci series, which is well known to mathematicians all over the world.

A certain man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair, which from the second month on becomes productive?

The resulting sequence is: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. Each number in the sequence is constructed simply by summing the last two numbers in the sequence. This is the first recursive number sequence known in Europe. A French born mathematician, Albert Girard, 1634, wrote the formula for the sequence:

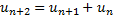
Robert Simpson, 1753 at the University of Glasgow noted that the ratio of consecutive Fibonacci numbers approaches the Golden Ratio as you go higher in the sequence.

Fascination

Fibonacci numbers are the sequence resulting from starting with 1,1 and then creating the next number in the sequence by summing the last two in the sequence:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377……..

I like the following representation:

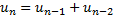
Robert Simpson’s observation (1753) is:

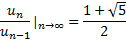
As we go further and further in the sequence, the ratio of two successive terms gets closer and closer to the Golden Ratio.

Fibonacci numbers show up often in nature. For example: the number of petals on a flower, or the number of scales on a pineapple or a pinecone are most often Fibonacci numbers. In the case of the pineapple you’ll note that the scales are in the form of two interlocking spirals. These spirals contain consecutive fibonacci numbers of scales. An implication of this is that the features we see in nature are not entirely coded in the DNA, but rather the DNA codes for processes, which are constrained such that the Fibonacci numbers appear as solutions due to the constraints. Constraints, such as closest packing and the dynamics of growth, could force such a preponderance of Fibonacci numbers.

These numbers were all a result of beginning with the seeds: 1, 1, and then applying the formula, where each element in the series is the sum of the last two elements.  What happens if you start with a different seed?  What happens when you change the formula?