The Five Platonic Solids

At Least as Exciting as a Platonic Relationship

A look at symmetry, regular polygons, platonic solids, and the Euler Characteristic

Let’s start by playing a little game with symmetry. Symmetry is one of the characteristics of objects and ideas that humans seek and find beautiful. We even find symmetry in facial features very appealing. In this game we are going to consider symmetry of geometric objects and ideas.

If we start our game with 0, “zero” dimensions, the only object we have to play with is a point. I’m not sure how to evaluate the symmetry of a point. Symmetry usually involves rotations and different points of view, but it is very hard to rotate anything in or with zero dimensions. Moving up the dimension ladder, the objects we have available in 1 dimension are lines. Again, I don’t have an intuitive feel for symmetry in one dimension. Now, when we go to two dimensions we have a familiar world to work with. In this case, let’s use our one dimensional lines on a two dimensional plane to create “regular shapes” or “regular polygons”. Regular polygons are shapes that have edges (formed by lines) that are all the same length and enclose an area on our 2-D plane.

The smallest number of straight lines I can use to enclose an area on the plane is 3.So, my “smallest” 2-D regular shape is a triangle.

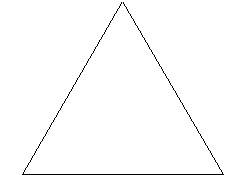
Triangles have a 3-fold symmetry. As we rotate the triangle one full rotation in the 2-D plane we find 3 distinct, evenly separated angles of rotation at which our triangle is indistinguishable from the non rotated state. If we rotate the triangle 1/3 of a full rotation we have a triangle that looks just the way it did when we started, assuming you didn’t go adding a color dimension to your triangle. Note that our triangle has 3 vertices at which pairs of lines connect. It also has 3 edges.

Of course, we have four-fold symmetry with a square. Now we have 4 vertices and 4 sides or edges.

Next we have a pentagon.

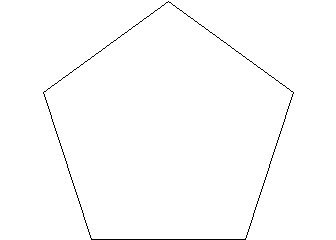
5 fold symmetry and 5 vertices with 5 edges.

6 fold symmetry give us an Hexagon.

We can construct a 7 sided regular polygons.

8 sided (Octagon).

9 sided.

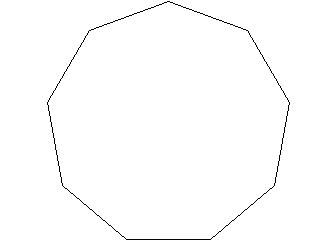
As a matter of fact, there seems to be no limit to the number of sides and vertices we can use to create regular polygons. If we go to infinite symmetry, we have a circle. No matter what angle you rotate the circle in the plane it appears exactly as it did before rotation. Our circle could be composed of an infinite number of straight lines, all infinitesimally short.

Our next step in this game is to use these regular polygons to create “regular” three-dimensional shapes

The most symmetric 3-D shapes are the Platonic Solids, which are formed by using regular polygons for the faces of these shapes. Each solid is enclosed by regular polygonal faces indistinguishable from each other. In other words, these are regular polyhedra. As we form these regular polyhedra, we will discover some rather interesting limits to our game.

Let’s start with triangular faces. When building a solid with triangular faces we have to figure out how it will go together. Each triangular face will have to share each of it’s edges with another triangle and each vertex will have to be shared by at least 3 triangular faces.

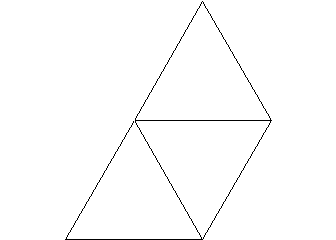
In this picture above we have the three faces that share one vertex. We can fold this plane at the shared edges and we move out of the plane to begin creating a 3-D object. With only one more triangle, four faces total, we can create a tetrahedron.

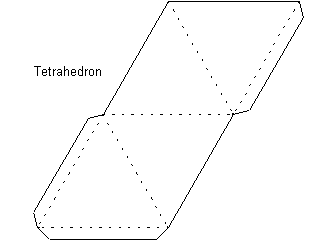
Click Here to get a pdf file that you can cut out and fold into a tetrahedron.

We can also create a solid with four triangular faces sharing a vertex.

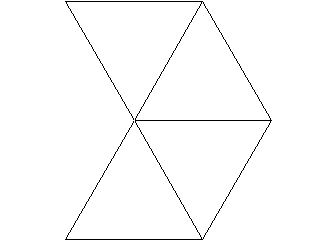
If we fold this plane object we get a 3-D object with an open square base, a bottomless pyramid. To create a true, closed solid we can use two of these and join them together at the open square base. The object is called an octahedron, an eight-sided object with identical triangular faces.

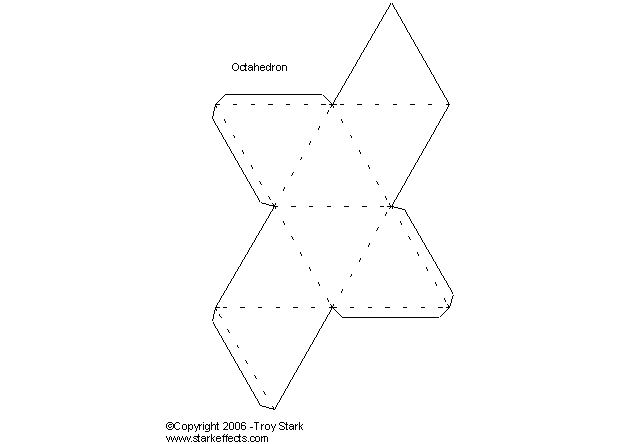
Click here to get a pdf file you can cut out and fold to make an octahedron. The octahedron looks like two square based pyramids attached at the square bases.

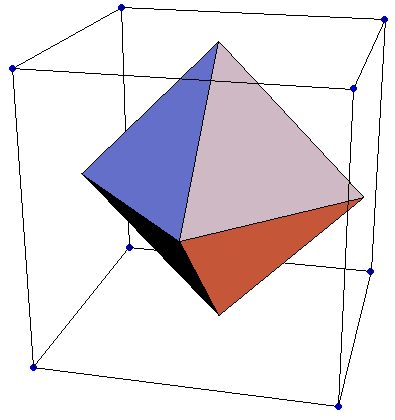
Now, we can try to create a solid object with triangular faces such that five faces share a vertex.

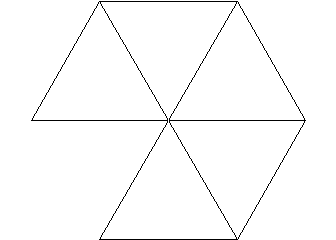
It takes four copies of this figure to fold into an Icosahedron having 20 triangular faces.

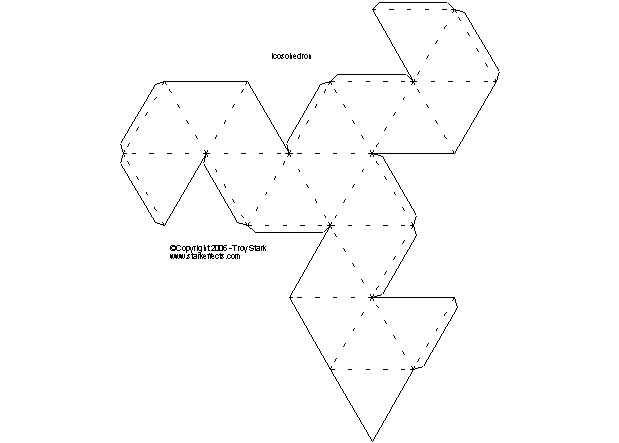
Click Here for a pdf file that you can cut out and fold into an icosahedron.

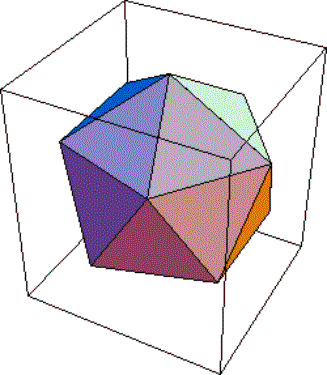
Here is something very cool! The vertices of an icosahedron are located on the corners of golden rectangles.

(0, ±1, ±φ)

(±1, ±φ, 0)

(±φ, 0, ±1)

where φ = (1+√5)/2 is the golden ratio

If we try to go one more step, we find a little problem. If we try to create a solid with triangular faces such that 6 triangles share a vertex, we can get this two dimensional figure:

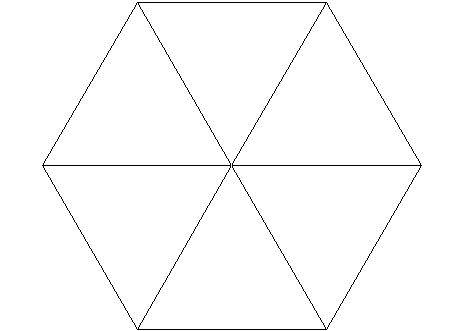
It won’t work!

Which, of course, is a perfectly good figure in two dimensions but there is no way to fold this into the third dimension. The triangles already take up all the 2-D space! We simply can’t create a 3-D regular polyhedron with triangular faces having 6 faces share a vertex.

Note that the angle inside each equilateral triangle is 60° so that having 6 triangle share a vertex takes up all 360° and we can’t move into the third dimension.

Alright, let’s move onto using a different regular polygon for the face. After the triangle, the next step is the square. We need at least 3 squares to share a vertex in order to fold into a three dimensional regular polyhedron.

This will work for forming a cube, or hexahedron (6 faces).

Click Here for a pdf file that you can cut out and fold up into a hexahedron (cube).

Now if we try to form a solid with square faces such that 4 faces share a vertex, we run into the same problem we did when we tried to get 6 triangles. The squares, with 90° interior angles, fill the entire 360° so that they can only lay flat and we have thus hit our limit.

This won’t work

Next, let’s try pentagonal faces, and, of course, we’ll start with three faces sharing a vertex.

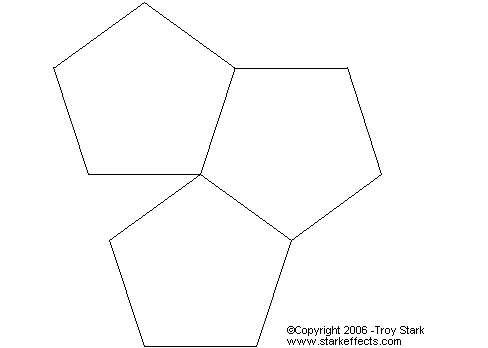
It is fairly obvious that we will not be able to go any further than three pentagons to a vertex, there is no more space to put another pentagon sharing the vertex. But, we can use these three. The solid we get is a Dodecahedron.

Here is a 2-D layout that can be folded into a Dodecahedron:

Or you can Click Here for a *.pdf version to print which can be cut out and folded into a Dodecahedron.

SOLID	VERTICES	EDGES	FACES	FACE SHAPE
Tetrahedron	4	6	4	Triangle
Hexahedron	8	12	6	Square
Octahedron	6	12	8	Triangle
Dodecahedron	20	30	12	Pentagon
Icosahedron	12	30	20	Triangle

Now we find that we have completely run out of possible Platonic Solids. There are only five possible. This is because we used triangles first and found only three possible Platonic solids that could be made with triangular faces. These were the Tetrahedron with 3 faces per vertex, the Octahedron with 4 faces per vertex and the Icosahedron with 5 faces per vertex. When we tried more than 5 triangular faces per vertex, we found that all of the 2-D space was filled with the triangular regular polygons so that there was no way to fold into 3-D space, they lie flat. We found only 3 square faces per vertex were possible, forming the Hexahedron (or cube) and we filled the entire 2-D space when we tried to use 4 square faces per vertex, they lie flat again. Then we found that only 3 Pentagonal faces per vertex were possible forming the Dodecahedron and we more than filled the 2-D space when we tried to fit 4 Pentagonal faces per vertex, they won’t even lie flat, we would have to fold each face itself. Now if we try using hexagonal faces, we find that we can’t even use 3 per vertex, since 3 Hexagons to a vertex already use up all of the 2-D space and we can’t fold into 3-D.

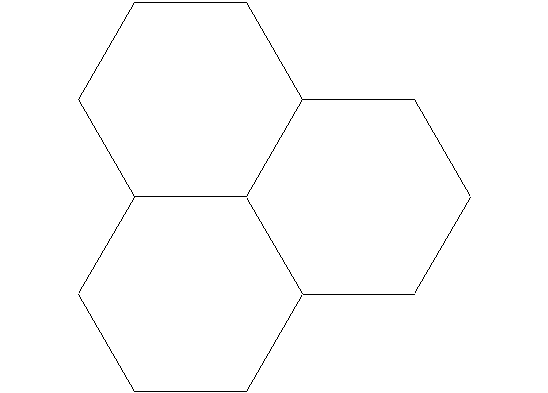
3 Hexagons Won’t Work

Every higher polygon will use up more than all of the 2-D space with just 3 polygons, since the angles between sides are even larger than on the hexagon. So we have found all five possible Platonic Solids.

Euler Characteristic

Let’s take a look at something else interesting related to this limitation. Take a pencil and on a piece of paper, with your eyes closed, draw a random line squiggling all over the paper. Put a dot at each place where the line crosses itself and at the beginning and ending points. Count the number of dots and call them vertices and assign this number to the variable V for vertices. Count the lines between vertices and assign this number to the variable E for edges. Now count the number of distinct regions created by your squiggly line drawing and include the region outside the drawing as one. Assign this number to the variable F (number of regions).

Now here is something magical, I can tell you that V-E+F=2. This number is always 2. Prove it to yourself by starting with the simplest drawing you can make and count V, E and F and you will find V-E+F=2 and then make another more complicated one and then a more complicated one and then you will see that as you create vertices and regions and edges you always maintain this relationship called the Euler Characteristic V-E+F=2.

Now let’s take a look at the Platonic Solids. They have the same characteristic!

SOLID	VERTICES (V)	EDGES (E)	FACES (F)	V-E+F
Tetrahedron	4	6	4	2
Hexahedron	8	12	6	2
Octahedron	6	12	8	2
Dodecahedron	20	30	12	2
Icosahedron	12	30	20	2

Now take a look at this, let S be the number of sides in each region (face), let C be the number of edges emanating from each vertex (the same for each vertex in a regular solid). Then the number of edges in the regular solid is 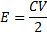since each edge is shared by 2 vertices. If we multiply the number of faces F, by the number of sides per face S, then divide by the number of edges per vertex, C, then we get the number of vertices, V.

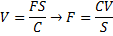
Now we can see that:

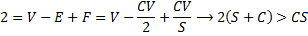
So now, we can see that 2 times the sum of the Sides per face and the edges per vertex must be greater than the product of the sides per face and the edges per vertex. In that case we see that 2(3+3)>3×3 which corresponds to a tetrahedron, 2(3+4)>3×4 which corresponds to an octahedron, 2(3+5)>3×5 which corresponds to an icosahedron and when we try 2(3+6) = 3×6 the greater sign didn’t apply and we don’t have a Platonic Solid with triangular faces and six faces per vertex. We also see 2(4+3)>4×3 which corresponds to a hexahedron (cube) but 2(4+4)<4×4 and 2(5+3)>3×5 which corresponds to a dodecahedron but 2(5+4)<5×4.

So, the Euler Characteristic can be used to deduce that there are only 5 possible Platonic Solids.

---